Thue - Morse - Prouhet Sequence
Posted on Sat 29 October 2016 in misc
I have a confession of sorts to make. As a little kid, when I wasn't chasing dragonflies or playing carroms or scribbling my name everywhere, I used to be engrossed in this rather weird game.
Story Time
I would start by doing something trivial using one of my hands, say my left hand. It could be flicking, tapping, touching something, whatever, something very trivial. I would call this a. I would then do something similar with my right hand and call it b.
So as to compensate the imbalance caused in the universe due to that ghastly act a. There now, the world is at peace with itself. Is it though?
a b
Balanced but not fair. Discernible folks would've realized by now that it isn't fair on b though right? I mean shouldn't it get a chance to lead the sequence too?
I would therefore, repeat b and then a. We have thus arrived at
a b b a
Justice seems to have prevailed and balance in the universe is as good as ever. Maybe not, after all. I mean b is kinda relieved with the court order but it still sees some injustice that has escaped the jury's attention. 'Justice of first order schmirst order.' b sneers at you, seething with discontent. Onlookers whisper among themselves 'Utter drivel. Token justice. Pandering to the powerful. Isn't b worthy enough to lead a sequence of length four?'
I would therefore proceed ahead with baab , baab and abba and thus complete
abba baab baab abba
Normally this is where it ended. gasp Slow Clap time. b is happy now guys. We did it. Look at the smile plastered on it's face. Some of you champions of the oppressed might say b isn't exactly beaming with joy but let's not get greedy and talk about justice of third order. [ abbabaabbaababba baababbaabbabaab baababbaabbabaab abbabaabbaababba ] That would be unfair on me, the attorney who took this up pro bono.
The nomenclature part came later of course. When it started, it was all about balancing it out and being fair. By fair I mean, why does *a have to be chosen first before b ? So ba gets appended to ab* and so on.
I can assure you it didn't look as bad as it sounds. I had perfected this game to an extant that If you had ever seen me doing it, you'd have assumed that I was just tapping my fingers to some rhythm and never would've guessed that I was going OCD there. ( unless of course one of a or b was 'picking my nose' or 'licking my lips' )
OCDCDODOC
Anyway, this wasn't something that consumed me or interfered with my everyday life, like how it plays out for people with debilitating OCD. And over the course of time, it skipped my mind completely as I developed new avocations like
- Summing the digits on number plates to test divisibility by 9
- Rearranging sentences based on syllable and character counts.
- Replacing soft consonants ( Saralas ) with hard consonants (Parushas) and vice versa. Kattappa --- Gaddabba
- Piecewise semantic conjugation of phrases and sentences. He is interesting --- She was boring
- Forcefully fitting a phrase/word into 5 syllables so that I can count it off my fingers. He yers my Hoo li badge -- Heers my Hoo li badge
I remembered the abba game again during my brief stint at Chennai Mathematical Institute and explored the possibility of the set of these sequences being a group under piece wise addition. Googling abbabaabbaababba to find if someone has worked on this before led me to this sequence, something that was discovered over one fifty years back and the astounding fact that this sequence has a history of being discovered over and over again by many people, including a chess grandmaster!
The Thue–Morse sequence was first studied by Eugène Prouhet in 1851, who applied it to number theory. However, Prouhet did not mention the sequence explicitly; this was left to Axel Thue in 1906, who used it to found the study of combinatorics on words. The sequence was only brought to worldwide attention with the work of Marston Morse in 1921, when he applied it to differential geometry. The sequence has been discovered independently many times, not always by professional research mathematicians; for example, Max Euwe, a chess grandmaster, who held the world championship title from 1935 to 1937, and mathematics teacher, discovered it in 1929 in an application to chess: by using its cube-free property (see above), he showed how to circumvent a rule aimed at preventing infinitely protracted games by declaring repetition of moves a draw.
I know! It made me feel kinda special. It felt as if the forces of evolution chose me to ~~kill John Lennon~~ unravel deep structures in the universe or something to that effect. Thanks to the internet however, I understood there are a good number of people who seem to have experienced this sequence playing in their heads during their childhoods. It's almost as if some people are hardwired to discover this pattern. I'm tempted to attribute it to some kind of OCD gene/mutation whatever but my lack of expertise on that subject prevents me from doing so. Whatever be the case, it is incredibly fascinating to see it manifest like this.
Equitable Distributions
This sequence, called Thue - Morse sequence or should I say Thue - Morse Morse - Thue sequence has many interesting properties.
It can be used as a quick and dirty, not necessarily optimal, algorithm to divide resources equitably among two people. Consider the case of two captains having to pick players for their respective teams from a pool of players. The teams need to be as evenly balanced as possible in terms of the cumulative strengths of the players. Both the captains have an idea of how good each player from the lot is.
The classical way of each captain choosing alternately, doesn't exactly bode well for the captain who gets to choose second. As you can see, the captain who gets to choose first will end up with the \({1}^{st}, {3}^{rd},{5}^{th}, {7}^{th}....\) best players of the lot whereas the other captain has to settle with the \({2}^{nd}, {4}^{th},{6}^{th}, {8}^{th}....\) best of the lot. If the captains agree to choose the players in Thue Morse pattern, in other words, if they take turns in taking turns in taking turns and so on, the distribution will be fairer. In this case the first captain gets the \({1}^{st}, {4}^{th},{6}^{th}, {7}^{th},{10}^{th},....\) best of the lot and the second one gets the \({2}^{nd}, {3}^{rd},{5}^{th}, {8}^{th},{9}^{th},....\) best of the lot.
Obviously, this doesn't work well if there are extreme outliers in the player pool. Elementary arithmetic shows that if the strengths of these players vary linearly, Thue - Morse distribution works to perfection.
Say we have a lot of \(8\) players, whose strengths decrease linearly from \(8\) to \(1\) when sorted in decreasing order. It can easily be seen that when the teams are split using Thue - Morse sequence, cumulative strengths of both the teams equal \(18\)
Note that we kept it simple by ignoring the existence of say bonding coefficients between players, you know the kind of thing that makes the sum of parts lesser/greater than the collective whole. We would then be looking at the problem of equi-partitioning a set into two groups with minimal difference between their quantified collective capabilities that are expressed as functions of bonding coefficients.
Other example I could think of
- Two parties taking turns for a titular post, if the magnitude of benefits that can be reaped using power decreases with the passage of time or benefits beget more benefits ( interest on money for example )
Koch Curve
The Thue - Morse sequence is also connected to the ubiquitous Koch curve ( snowflake curve ). The fun never ends I tell you. You can generate it using the following simple algorithm.
For every element in the Thue - Morse sequence, if the element is \(a\), move forward by one unit and turn anticlockwise by \(60^{\circ}\) if the element is \(b\). As simple as that.
Generating Thue - Morse Sequences
Time for formalization.
There are many ways of generating the Thue - Morse sequence.
Mirror method
Let's start with the way it played in my head.
Let \(f(a,b,n)\) represent the sequence in my head of \({n}^{th}\) order. I generated it using the equation \(f(a,b,n) = f(a,b,n-1) + f(b,a,n-1) + f(b,a,n-1) + f(a,b,n-1)\)
where + represents concatenation and \(f(a,b,1) = abba\)
The Thue - Morse sequence, on the other hand, starts with \(a, ab\) and consists of \(abbabaab\) between \(abba\) and \(abbabaabbaababba\). My sequence turns out to be a sub sequence of Thue - Morse sequence. To be more specific, it comprises all the odd terms starting from \(abba\).
The right recursive relation that describes Thue - Morse sequence of \({n}^{th}\) order is thus \(f(a,b,n) = f(a,b,n-1) + f(b,a,n-1)\)

It can be generated as follows in Python.
def f(a,b,n):
if n == 0:
return a
else:
return f(a,b,n-1) + f(b,a,n-1) if n > 1 else a + b
Please note that, in literature, there is no such thing as a Thue - Morse sequence of \({n}^{th}\) order. There is only one Thue - Morse sequence and is equal to \(\lim_{n\rightarrow \infty }f(a,b,n)\)
Sum of binary digits
Let \(s(n)\) denote the sum of digits of binary representation of \(n\)
\(t_n\), the \({n}^{th}\) term of \(\lim_{n\rightarrow \infty }f(0,1,n)\) is then equal to \(s(n)\hspace{1 mm} mod\hspace{1 mm} 2\)
Proof by induction
\(f(0,1,0)\hspace{1 mm}=s(0)\hspace{1 mm} mod\hspace{1 mm} 2\hspace{1 mm}=0\)
So the statement is true for \(n\hspace{1 mm}=\hspace{1 mm}0\)
Let's assume it is true for all \(m\hspace{1 mm}<\hspace{1 mm}n\)
Let \(2^k \hspace{1 mm}\leq n\hspace{1 mm}<\hspace{1 mm} 2^{k+1}\)
\(\rightarrow \hspace{5 mm}t_n\) is the \(n^{th}\) term of \(f(a,b,k+1)\)
\(\rightarrow \hspace{5 mm}t_n\) is the \(n^{th}\) term of \(f(a,b,k)\hspace{1 mm}+\hspace{1 mm}f(b,a,k)\)
\(\rightarrow \hspace{5 mm}t_n\) is the \({(n-2^{k})}^{th}\) term of \(f(b,a,k)\)
Since \(f(b,a,k)\) is the mirror image of \(f(a,b,k)\), we can conclude
\(t_n \hspace{1 mm}=\hspace{1 mm}(t_{n-2^{k}} + 1)\hspace{1 mm}mod\hspace{1 mm}2\)
By induction we have \(t_{n-2^{k}}\hspace{1 mm}=\hspace{1 mm}s(n-2^{k})\hspace{1 mm}mod\hspace{1 mm}2\)
Also, since \(2^k \hspace{1 mm}\leq n\hspace{1 mm}<\hspace{1 mm} 2^{k+1}\), we have \(s(n)\hspace{1 mm}=\hspace{1 mm}s(n-2^{k})\hspace{1 mm}+\hspace{1 mm}1\)
If the last step isn't obvious, see how it is true for numbers represented in decimal system.
\(\rightarrow \hspace{5 mm}t_n\hspace{1 mm}=\hspace{1 mm}((s(n)-1)\hspace{1 mm}mod\hspace{1 mm}2\hspace{1 mm}+\hspace{1 mm}1)\hspace{1 mm}mod\hspace{1 mm}2\)
\(\rightarrow \hspace{5 mm}t_n\hspace{1 mm}=\hspace{1 mm}s(n)\hspace{1 mm}mod\hspace{1 mm}2\)
The following Python function returns the first \(n\) characters of the Thue - Morse sequence using the above method. This is a better function for generating the sequence since it doesn't compute \(f(a,b,0), f(a,b,1), f(a,b,2),..., f(a,b,n-1)\) for generating \(f(a,b,n)\)
def f(a,b,n):
p = ''.join([str(sum_of_digits(number) % 2) for number in range(n)])
return p.replace('0',a).replace('1',b)
def sum_of_digits(number):
return sum([int(numeral) for numeral in str(bin(number))[2:] ])
Morphism method
Simply put, a morphism is a structure preserving function on a mathematical object under some particular operation.
In our case, the operation is concatenation denoted by \(+\). So if \(m(x)\) is such a structure preserving function under concatenation over strings, we have \(m(x+y)\hspace{1 mm}=\hspace{1 mm}m(x)\hspace{1 mm}+\hspace{1 mm}m(y)\hspace{1 mm}=\hspace{1 mm}m(x)m(y)\)
Define a Thue - Morse morphism \(m\) such that \(m(a) = a+b=ab, m(b) = b+a=ba\)
\(\rightarrow \hspace{5 mm} m^{2}(a) = m(m(a)) = m(ab) = m(a) + m(b) = ab + ba = abba\)
\(m^{3}(a) = m(m(m(a))) = m(m(ab)) = m(abba) = m(a) + m(b) + m(b) + m(a) = abbabaab\)
and so on. You can see that it is the same as \(f(a,b,3)\) defined earlier.
Similarly, it can be seen that \((m^{2}(b)\) and \(m^{3}(b)\) are equal to \(f(a,b,2)\) and \(f(a,b,3)\) respectively.
We can prove that is indeed the case till death does them apart using induction.
We've just proved that the statement is true for \(n=1, 2,3\)
Assume it is true for \(n\).
\(m^{n+1}(a)\hspace{1 mm}=\hspace{1 mm}m^{n}(m(a))\) \(=\hspace{1 mm}m^{n}(ab)\) \(=\hspace{1 mm}m^{n}(a)+m^{n}(b)\) \(=\hspace{1 mm}f(a,b,n)+f(b,a,n)\) \(=\hspace{1 mm}f(a,b,n+1)\)
Similarly, it can be proved that \(m^{n+1}(b) = f(b,a,n+1)\)
Below is the Python code for generating Thue - Morse sequence using this method.
def m(x, a, b):
if len(x) == 1:
if x == a:
return str(a) + str(b)
if x == b:
return str(b) + str(a)
if len(x) > 1:
return ''.join([m(element, a, b) for element in x])
def m_n(x,a,b,n):
m_n = a
for element in range(n):
m_n = m(m_n,a,b)
return m_n
Recursion
The Thue - Morse sequence can also be generated using the following recurrence relation.
\(t_0\hspace{1 mm}=\hspace{1 mm}0\)
\(t_{2n}\hspace{1 mm}=\hspace{1 mm}t_n\)
\(t_{2n+1}\hspace{1 mm}=\hspace{1 mm}1-t_{2n}\)
Using the recursive relations mentioned above, we can generate the sequence in Python as follows
def tn(n):
if n == 0:
return 0
return tn(n/2) if n % 2 == 0 else 1 - tn(n-1)
def f(a,b,n):
return ''.join([str(element).replace('0',a).replace('1',b)
for element in [tn(index) for index in range(n)]])
Infinite Product
The \(n^{th}\) term of Thue - Morse sequence can also be determined by calculating the sign of coefficient of \(x^n\) in the following infinite product.
Miscellaneous
Found these formulations on a Facebook group dedicated to Atomic functions, Self-differential equations and Morse -Thue sequences.
Apparently, the first formulation involving Hyper Geometric functions simplifies to the second.
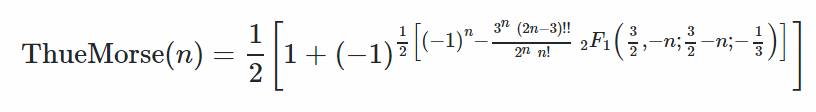
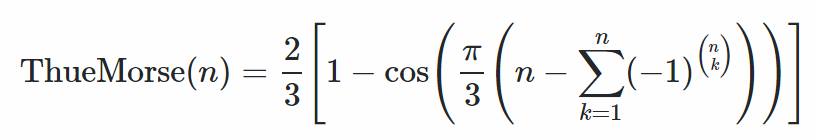
N - variable Thue - Morse sequence
How about a generalized Thue - Morse sequence comprising \(n\) variables? I haven't found any literature on the internet concerning this but I suppose a man can dream!
Let's try it out for \(3\) variables - \(a,b,c\).
My intuition tells me cyclical permutations might just do the trick. Let's explore that.
abc
abc-bca-cab
abc-bca-cab bca-cab-abc cab-abc-bca
How do I know if this is structurally similar to the two variable Thue - Morse sequence apart from the fact that my gut feeling says so?
My sophomoric knowledge of mathematics not withstanding, I can't think of a way to tackle this problem properly. A simple hack however, might just do the job ( sort of ). Remember the fair distribution property of Thue - Morse sequence and how it worked like a charm when the players' competency function was linear? Let's consider the case of picking three balanced teams out of \(9\) players whose strengths vary from \(9\) to \(1\) linearly and see how this sequence fares.
Team 1 comprises \(1^{st}, 6^{th}, 8^{th}\) best players, Team 2 comprises \(2^{nd}, 4^{th}, 9^{th}\) best players and Team 3 comprises \(3^{rd}, 5^{th}, 7^{th}\) best players. So the respective strengths of the three teams are \(9+4+2\), \(8+6+1\) and \(7+5+3\)
Voila! There you have it. I can now speak with some confidence that this is indeed a Thue - Morse like sequence of three variables and postulate a general formula for n - variables with I suppose a little less confidence.
Extending the logic, morphism in this case would be \(m(a)\hspace{1 mm}=\hspace{1 mm}abc, m(b)\hspace{1 mm}=\hspace{1 mm}bca, m(c)\hspace{1 mm}=\hspace{1 mm}cab\)
A Thue - Morse like morphism of \(n\) variables will thus be \(m(a_1)\hspace{1 mm}=\hspace{1 mm}a_1a_2a_3....a_n, m(a_2)\hspace{1 mm}=\hspace{1 mm}a_2a_3....a_na_1,....., m(a_n)\hspace{1 mm}=\hspace{1 mm}a_na_1....a_{n-1}\)
Update
It appears that an even more generalized form of Thue - Morse sequence can be generated using a generalized version of the Binary digits' sum method.
The \(n^{th}\) term of the generalized Thue - Morse sequence \({t_{p,q}}^n\) can be arrived at as follows
\({t_{p,q}}^n\hspace{1 mm}=\hspace{1 mm}s_{p}(n)\hspace{1 mm}mod\hspace{1 mm}q\) for \(p ≥ 2\) and \(q ≥ 1\), where \(s_p(n)\) is the sum of of digits of \(n\) represented in base \(p\)
References
The ubiquitous Prouhet Thue Morse sequence
An overview of the Thue Morse sequence
The ubiquitous Thue Morse sequence - Talk by Jeffrey Shallit
Atomic functions, Self-differential equations and Morse -Thue sequences
